Zenón de Elea és un lògic i filòsof grec conegut principalment per les paradoxes anomenades en honor seu. No se sap gaire sobre la seva vida. La ciutat natal de Zenó és Elea. També en els escrits de Plató es va esmentar la reunió del filòsof amb Sòcrates.
Cap al 465 a.C. e. Zeno va escriure un llibre en què va exposar totes les seves idees. Però, malauradament, no ha arribat als nostres dies. Segons la llegenda, el filòsof va morir en una batalla amb un tirà (presumptament el cap d'Elea Nearch). Tota la informació sobre Elea es va recopilar mica en mica: a partir de les obres de Plató (nascuts 60 anys després Zeno), Aristòtil i Diògenes Laertius, que van escriure tres segles després un llibre de biografies de filòsofs grecs. Zeno també s’esmenta en els escrits dels representants posteriors de l’escola de filosofia grega: Themisty (segle IV A.D.), Alexander Afrodinsky (segle III A.D.), així com Philoponus i Simplicius (tots dos van viure al segle VI A.D.). A més, les dades d'aquestes fonts són tan coherents entre si que es poden reconstruir a partir d'elles totes les idees del filòsof. En aquest article us parlarem de les paradoxes de Zenó. Per tant, comencem

Paradoxes del plató
Des de l’època de Pitàgores, l’espai i el temps es consideraven exclusivament des del punt de vista de les matemàtiques. És a dir, es creia que estaven compost de molts punts i punts. Tanmateix, tenen una propietat més fàcil de intuir que de definir, és a dir, de “continuïtat”. Algunes paradoxes de Zenó demostren que no es pot dividir en moments o punts. El raonament del filòsof es refereix al següent: "Suposem que hem completat la divisió fins al final. Aleshores només una de les dues opcions és certa: o bé obtenim les quantitats mínimes possibles o parts indivisibles, però infinites en quantitat, o la divisió ens portarà a parts sense magnitud, ja que la continuïtat, sent homogènia, ha de ser divisible en qualsevol circumstància.. No pot ser divisible en una part, però no en l’altra. Malauradament, tots dos resultats són bastant ridículs. El primer es deu al fet que el procés de divisió no pot acabar mentre hi ha parts a la resta que tenen un valor. I el segon és perquè en una situació així, inicialment tot s'hauria format a partir del no-res ”. Simplicius va atribuir aquest argument a Parmènides, però és més probable que el seu autor sigui Zeno. Anem més enllà.
Paradoxes del moviment de Zeno
Es consideren a la majoria de llibres dedicats al filòsof, perquè entren en dissonància amb evidència dels sentiments de l’Eleatics. En relació al moviment, es distingeixen les següents paradoxes de Zenon: “Fletxa”, “Dichotomia”, “Aquil·les” i “Etapes”. I ens van venir gràcies a Aristòtil. Mirem de prop.
Fletxa
Un altre nom és la paradoxa quàntica de Zenó. El filòsof afirma que qualsevol cosa es queda parat o es mou. Però no hi ha res en moviment si l’espai ocupat és igual a la longitud. En un moment determinat, la fletxa en moviment es troba en un sol lloc. Per tant, no es mou. Simplicius va formular aquesta paradoxa de forma breu: "Un objecte volador ocupa un lloc igual a l'espai, però el que ocupa un lloc igual en l'espai no es mou. Per tant, la fletxa està en repòs. " Femistius i Phelopon van formular opcions similars.
"Dicotomia"
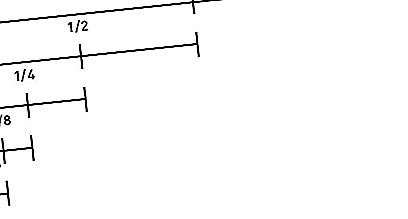
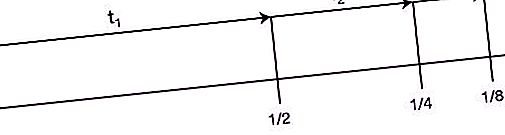
Ocupa el segon lloc en la llista de "paradògenes de Zenó". Es diu així: “Abans que un objecte que comenci a moure’s pugui recórrer una certa distància, ha de superar la meitat d’aquest camí, després la meitat de la resta, etc. fins a l’infinit. Com que durant les divisions repetides de la distància per la meitat, el segment es torna finit tot el temps i el nombre d'aquests segments és infinit, no es pot superar aquesta distància en un temps finit. A més, aquest argument és cert tant per a petites distàncies com per a velocitats elevades. Per tant, qualsevol moviment és impossible. És a dir, el corredor ni tan sols podrà començar ".
Aquesta paradoxa va comentar amb molt de detall Simplicius, indicant que en aquest cas s’ha de fer un nombre infinit de tocs en un temps finit. "Qualsevol que toqui qualsevol cosa pot comptar, però el conjunt infinit no es pot classificar ni comptar." O, segons va dir Philopon, un conjunt infinit és indefinible.
Aquil·les
També coneguda com la paradoxa de la tortuga Zeno. Aquest és l’argument filosòfic més popular. En aquesta paradoxa de moviments, Aquil·les competeix en una carrera amb una tortuga, que té un petit handicap al principi. La paradoxa és que la guerrera grega no podrà posar-se al dia amb la tortuga, ja que primer arribarà al lloc del seu inici, i ella ja estarà al punt següent. És a dir, la tortuga sempre estarà per davant d’Aquil·les.
Aquesta paradoxa és molt similar a una dicotomia, però aquí la divisió infinita va segons la progressió. En el cas d'una dicotomia, es va produir una regressió. Per exemple, el mateix corredor no pot començar, ja que no pot deixar la seva ubicació. I en la situació amb Aquil·les, encara que el corredor comenci a moure's, encara no vindrà a córrer enlloc.
"Etapa"
Si comparem totes les paradoxes de Zenó en termes de complexitat, aquest seria el guanyador. És més difícil que d’exposar-ne d’altres. Simplicius i Aristòtil van descriure aquest raonament fragmentàriament i no es pot basar en la seva fiabilitat amb un 100% de seguretat. La reconstrucció d’aquesta paradoxa té la forma següent: deixem que A1, A2, A3 i A4 siguin cossos immòbils d’igual mida, i B1, B2, B3 i B4 són cossos de la mateixa mida que els cossos A. B es desplacen cap a la dreta de manera que cada B passi. I en un instant, que és el període de temps més reduït de tots els possibles. Sigui B1, B2, B3 i B4 cossos idèntics a A i B, i es mouen en relació amb A cap a l’esquerra, superant cadascun dels cossos en un instant.
Bviament, B1 va superar els quatre cossos de B. Prenem per unitat el temps que va trigar un cos de B a passar per un cos de B. En aquest cas, es necessitaven quatre unitats per a tot moviment. Tot i això, es creia que els dos moments que va passar per aquest moviment eren mínims i, per tant, indivisibles. Es dedueix que quatre unitats indivisibles són iguals a dues unitats indivisibles.